Data and Model Fitting
Mathwrist Code Example Series

(October 5, 2023)

Abstract

This document gives some code examples on how to use the data and model fitting features in Mathwrist’s C++ Numerical Programming Library (NPL).

1 Nonlinear Least Square

Assme a nonlinear model function $f(t)=ae^{bt}$ with model parameters $a=0.02$ and $b=0.6$ . We have observed $(t_{i},y_{i}),i=0,\cdots 99$ where $y_{i}=f(t_{i})+\epsilon$ for some random noise $\epsilon$ . The following example illustrates using modified Gauss-Newton method to recover model parameters from the observation data.

1 // Model parameters used to populate some observation data.

2 constexpr double a = 0.02;

3 constexpr double b = 0.6;

5 // A vector valued function to compute residuals.

6 class Residual : public VtrValueFunctionND

7 {

8 std::vector<double> m_y;

9 std::vector<double> m_t;

11 public:

12 Residual()

13 {

14 for (double t = 0; t < 1; t += 0.01)

15 {

16 m_t.push_back(t);

18 // Generate some data noise

19 double noise = std::rand() * 0.001 / RAND_MAX;

21 // Populate observation data with noise.

22 m_y.push_back(a * std::exp(b * t) + noise);

23 }

24 }

26 void eval(const Matrix& x, Matrix* _v=0, Matrix* _J=0) const

27 {

28 size_t n = m_y.size();

30 // Model parameters recovered during calibration.

31 double a = x(0, 0);

32 double b = x(1, 0);

34 // Residuals

35 if (_v != 0)

36 {

37 assert(_v->row_size() == n);

39 Matrix::iterator_support its = _v->it_support();

40 assert(its.get() != 0);

42 Matrix::iterator_traits::col_iterator it =

43 its->col_begin(0);

45 Matrix::iterator_traits::col_iterator it_end =

46 its->col_end(0);

48 for (size_t i = 0; it != it_end; ++i, ++it)

49 {

50 *it = a * std::exp(b * m_t[i]) - m_y[i];

51 }

52 }

54 // Jacobian

55 if (_J != 0)

56 {

57 assert(_J->row_size() == n);

58 assert(_J->col_size() == 2);

60 Matrix::iterator_support its = _J->it_support();

61 assert(its.get() != 0);

63 Matrix::iterator_traits::col_iterator it1 =

64 its->col_begin(0);

66 Matrix::iterator_traits::col_iterator it2 =

67 its->col_begin(1);

69 for (size_t i = 0; i < n; ++i)

70 {

71 double temp = std::exp(b * m_t[i]);

72 *it1++ = temp;

73 *it2++ = a * temp * m_t[i];

74 }

75 }

76 }

78 size_t vector_size() const { return m_y.size(); }

79 size_t dimension_size() const { return 2; }

80 };

82 Residual residual;

84 NLS_GaussNewton newton;

86 // Initial guess x = 0

87 Matrix x(2, 1);

89 newton(residual, x);

90 assert(std::abs(x(0, 0) - a) < 0.001);

91 assert(std::abs(x(1, 0) - b) < 0.01);

Note that the calibrated model parameters at line 90 and 91 are not same as the true parameters because we added some random noise to the observation data.

2 Model Fitting

This example is an application of smooth curve fitting in finance industry. In finance, it is a common practice to build a smooth interest rate curve that is a 1-dimensional function wrt time, i.e. $r(t)$ . The discount factor $f(t)$ at time $t$ is computed from a nonlinear function $f(t)=e^{-r(t)t}$ . In this toy example, we assume $N$ discount factors are observed from the financial market at a list of time points $\{t_{i},f_{i}\},i=0,\cdots,N-1$ , i.e. $f_{i}=f(t_{i})+\epsilon$ for some data noise $\epsilon$ around 1.e-3.

The model fitting exercise here will use a cubic B-spline curve to represent the interest rate curve, $r(t;\theta)=\phi(t)^{T}\theta$ , where $\phi(t)$ is a vector of B-spline basis and $\theta$ is a vector of basis coefficients. Assume we choose B-spline knot points to be $[0,0.25,1,5,10,30]$ in time horizon. From the observed data $\{t_{i},f_{i}\}$ , we want to recover the model parameter $\theta$ hence obtain a smooth interest curve.

We choose to build the curve $r(t;\theta)$ by minimizing the curve roughness subject to discount factor fitting errors being within $1.e-3$ tolerance. In addition, we impose additional curve constraints to require the interest rates being positive at observed time points, i.e. $r(t_{i};\theta)\geq 0,i=0,\cdots,N-1$ .

1 // time in unit of years

2 const double t[12] =

3 {

4 0.083333333, 0.166666667, 0.25, 0.5, 1,

5 2, 3, 5, 7, 10,

6 20, 30

7 };

9 // a smooth curve of interest rates

10 const double r[12] =

11 {

12 0.0001, 0.0002, 0.0003, 0.0004, 0.0005,

13 0.0016, 0.0031, 0.0076, 0.0116, 0.0147,

14 0.0208, 0.0215

15 };

17 // The observed discount factors: exp(-rt) + some random noise

18 const double df[12] =

19 {

20 0.999837189, 0.999659956, 0.999875655, 0.999845438, 0.999600265,

21 0.996395796, 0.990311641, 0.962516537, 0.921680833, 0.863478084,

22 0.660144366, 0.524662124

23 };

25 // A residual function for these 12 observed time and

26 // discount factors.

27 class Residual : public VtrValueFunctionND

28 {

29 const double* m_df;

30 const double* m_t;

31 mutable BSplineCurve m_spline;

33 public:

34 Residual(

35 const double* _df,

36 const double* _t,

37 const BSplineCurve& sp) : m_df(_df), m_t(_t), m_spline(sp)

38 {

39 }

41 void eval(const Matrix& x, Matrix* _v = 0, Matrix* _J = 0) const

42 {

43 // x is the vector of spline basis coefficients to calibrate.

44 ftl::Assert(x.row_size() == this->dimension_size());

45 m_spline.set_basis_coeff(x);

47 if (_v != 0)

48 {

49 ftl::Assert(_v->row_size() == 12);

51 for (size_t i = 0; i < 12; ++i)

52 {

53 // interest rate from the B-spline curve

54 double r = m_spline.eval(m_t[i]);

56 // Fitting error

57 (*_v)(i,0) = std::exp(-r * m_t[i]) - m_df[i];

58 }

59 }

61 // Jacobian by finite difference.

62 if (_J != 0)

63 {

64 ftl::Assert(_J->row_size() == 12);

65 ftl::Assert(_J->col_size() == x.row_size());

66 this->jacobian_fwd_diff(x, *_J, _v);

67 }

68 }

70 size_t vector_size() const { return 12; }

71 size_t dimension_size() const { return m_spline.basis_coeff().size(); }

72 };

74 // B-spline knot points.

75 double t_knots[] = { 0, 0.25, 1, 5, 10, 30 };

77 // Create a cubic spline curve fitting solver with 6

78 // knot points. Also set curve value constraints to

79 // be positive at all 12 time data points.

80 SmoothSplineCurve smooth_spline(t_knots, 6, 3, 12);

81 {

82 for (size_t i = 0; i < 12; ++i)

83 {

84 SmoothCurveFitting::Constraint c;

85 c.x = t[i];

86 c.type = SmoothCurveFitting::Constraint::VALUE;

87 c.value = Bound::lower(0);

88 smooth_spline.add_interior_constr(c);

89 }

90 }

92 // Set initial guess to a flat rate.

93 size_t n_params = smooth_spline.n_parameters();

94 Matrix beta(n_params, 1);

95 beta = 0.01;

96 smooth_spline.set_parameters(beta);

98 // Create the residual function by passing the time,

99 // discount factor and underlying spline curve.

100 Residual residual(df, t, smooth_spline.spline());

102 // Tolerance of fitting to discount factors.

103 Matrix tolerance(12, 1);

104 tolerance = 1.e-3;

106 smooth_spline(residual, tolerance, 100, true, 1.e-8, 0.01);

108 // This spline curve object can be directly plotted in GDE.

109 const BSplineCurve& spline = smooth_spline.spline();

111 // Check fitting errors.

112 for (size_t i = 0; i < 12; ++i)

113 {

114 double rate = smooth_spline.curve().eval(t[i]);

115 double disc = std::exp(-rate * t[i]);

117 ftl::Assert(std::abs(rate - r[i]) < 1.e-3);

118 ftl::Assert(std::abs(disc - df[i]) < 1.001e-3);

119 }

Note that at line 104, we set the discount factor fitting error tolerance to be 1.e-3, same magnitude as the noise that we artificially added to observation data. Setting the tolerance too small will be fitting to the noise. In practice, financial professionals have good knowledge on how tight market data should be fit.

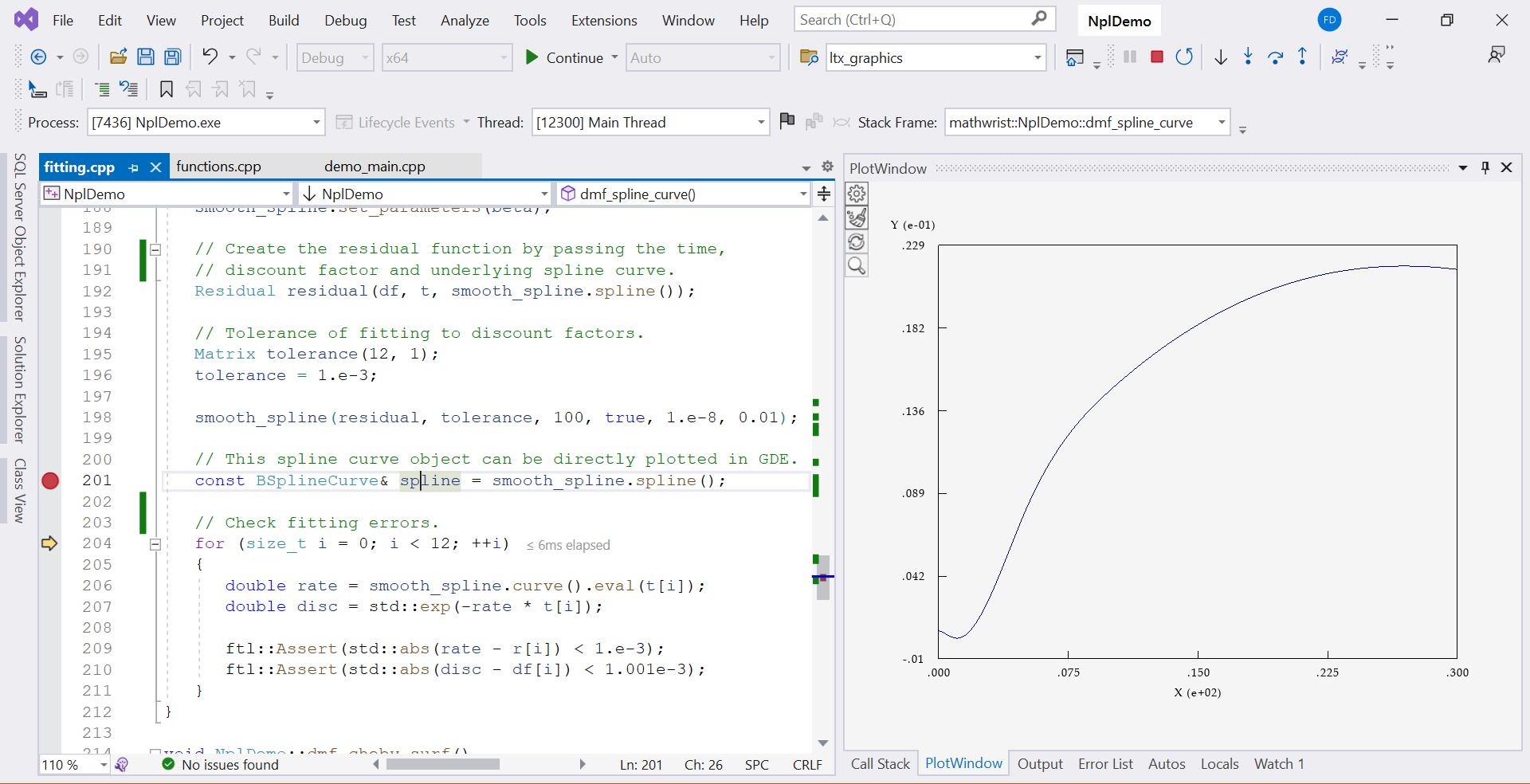
After calibration, we can retrieve the smooth spline curve at line 109. This curve object is recogonized by GDE and can be plotted as illustrated in Figure 1.

Data and Model Fitting Mathwrist Code Example Series

Abstract

1 Nonlinear Least Square

2 Model Fitting

Data and Model Fitting
Mathwrist Code Example Series