Differential Equations
Mathwrist Code Example Series

The HIRES benchmark test problem refers to “High Irradiance RESponse”. It originates from plant physiology and describes how light is involved in morphogenesis. It is a stiff nonlinear ODE system of 8 equations,

The solution at $T=321.8122$ is,

Since the HIRES problem is nonlinear, at line 2 we create a struct Hires derived from NPL’s general ODE interface class ODE. Lines 4 to 6 implement base class virtual functions to specify the ODE’s size, start and end time. We supply an implementation of the y_prime virtual function from line 9 to 20 to compute $y^{\prime }(t)$.

At line 45, we create an IDeC solver to use $𝒪(h)$ explicit base method and spectral IDeC. We further instruct IDeC to use an approximation polynomial of degree 7 and 3 error correction iterations. On a laptop with 2.60GHz CPU and 8.00 GB RAM, this problem is solved in less than 0.02 seconds with absolute error tolerance smaller than 3.e-12. In comparable time and machine setup, this result is 2 order more accurate than the benchmark result on SciML Benchmark and Test Set for IVP Solvers.

This is an example of linear ODE to demonstrate NPL’s implicit IDeC method. The problem is defined as the following:

It has an analytic solution

At line 2, we now derive from NPL’s linear ODE interface ODE_Linear and define the behavior of this ODE via a set of virtual functions. For large linear ODE systems, $A(t)$ often is a sparse matrix. NPL allows users to store $A(t)$ in a user-designed compact form. The size_A virtual function is used by IDeC solvers to allocate correct memory storage for matrix $A(t)$. In this particular example though, $A(t)$ is a constant $2\times 2$ matrix. We let the size_A() function return 0 at line 12. This instructs IDeC solvers not to allocate memory to store $A(t)$.

From line 15 to 22, we supply an implementation to compute $y^{\prime }(t)$. This is a virtual function indirectly inherited from the ODE base class. In addition, we also need implement virtual functions directly inherited from ODE_Linear class. Line 28 to 32 is the implementation to compute $A(t)$ and $s(t)$ as of time $t$. Because we have instructed IDeC solvers that $A(t)$ has 0 size, a nullptr will be passed from the solver to the second parameter of the update function. We ignore this parameter and only compute $s(t)$. Similarly, if the ODE is homogeneous, IDeC will pass nullptr to the third parameter of update function.

From line 37 to 49, we solve an linear system $\left(𝐈-h𝐀(t)\right)𝐲=𝐫$ for some right hand side (rhs) vector $𝐫$. It is users’ responsibility to solve this equation based on their choice of the compact form of $A(t)$. Again, because $A(t)$ is not stored at IDeC solver side, the first parameter passed to this function is a nullptr. Since $A(t)$ is constant here, we also ignore the second parameter $t$ in this function. The function body simply inverts the system and save result back to buffer pointer _y.

Lastly, line 52 to 60 computes $y^{\prime }(t)=A(t)y(t)+s(t)$ using a pointer to the compact storage of $A(t)$, which is a nullptr here as we explained. Pointer s will be nullptr for homogeneous system. Two Lambda functions at line 64 and 70 are the coefficient terms of the analytic solution $y(t)$. At line 96, we create a classic IDeC solver using interpolation polynomial of degree 6 and 3 number of error iterations. Because of the stability of implicit methods, we are able to solve the problem with a relatively large time step size.

In this example we have 2 unknown functions $v_1(t,x)$ and $v_2(t,x)$ that are governed by the same PDE and Dirichlet boundary conditions,

They differ from each other on the following initial values

, and have the analytic solutions

We will create different solvers to solve $v_1(t,x)$ and $v_2(t,x)$ simultaneously.

At line 4, we create a derived struct Heat under the PDEParabolic1D interface. From line 9 to 18, we implement the coefficient pure virtual function by filling the $f(t,x)$ coefficient buffer with constant $\frac{1}{4}$. Since we don’t have other coefficient terms in the PDE, we ignore the _gtx and _htx buffer pointer parameters.

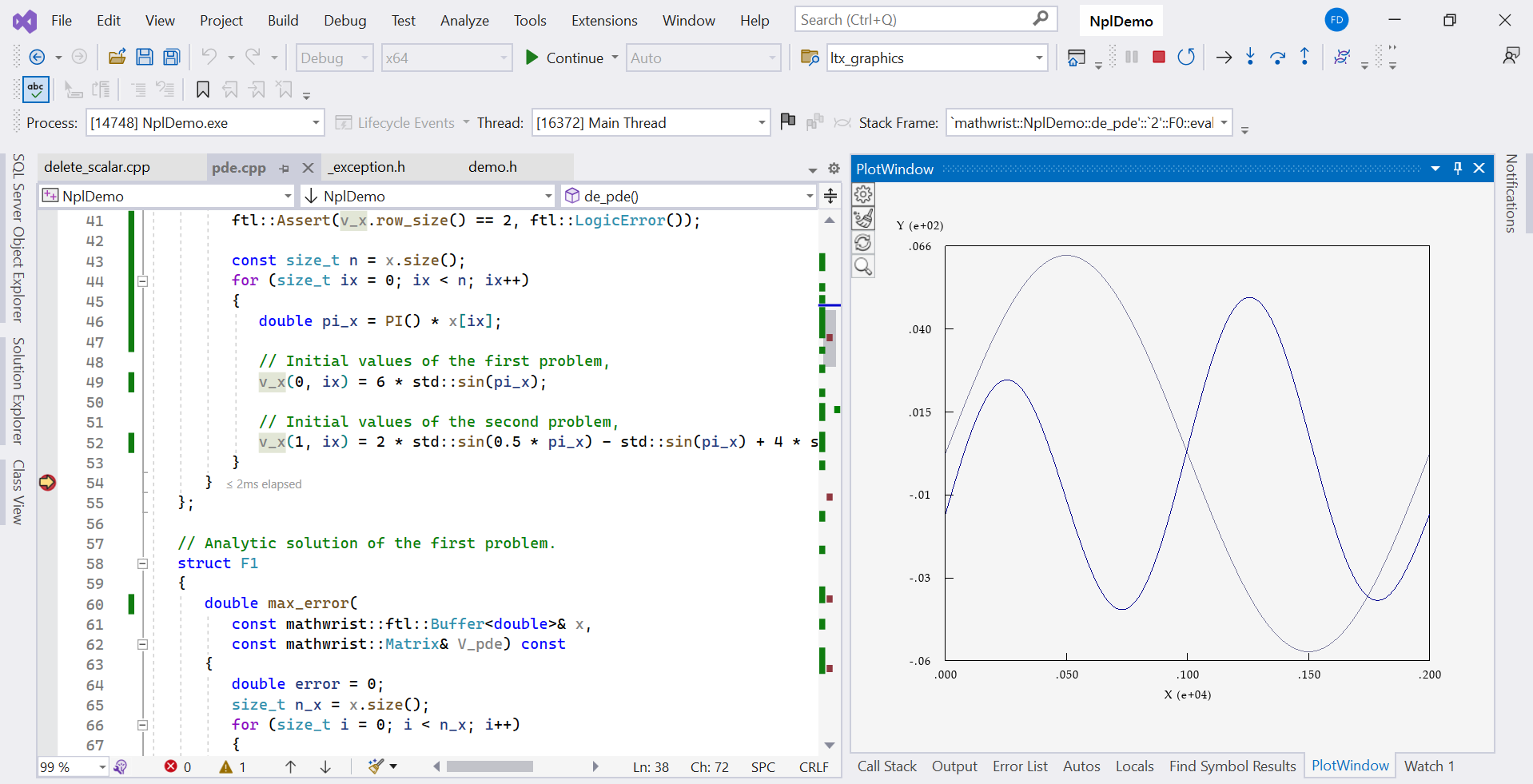
Struct F0 from line 24 to 44 implements the initial value function interface and fill $v_1(0,x)$ and $v_2(0,x)$ to 2 rows of the matrix parameter v_x in eval function. A plot of initial values can be viewed from GDE plot window illustrated in Figure 1. Struct F1 and F2 implement the analytic solution of $v_1(t,x)$ and $v_2(t,x)$ respectively.

Between line 98 and 102, we implement the Dirichlet boundary condition. Line 113 and 114 create a PDE problem specification object, where we specify that there are 2 problems to be solved together. Code block 117 to 132 uses Crank-Nicolson method. The numerical solutions are stored in 2 separate rows of the vx matrix parameter on return. We then check the solution error from line 127 to 131.

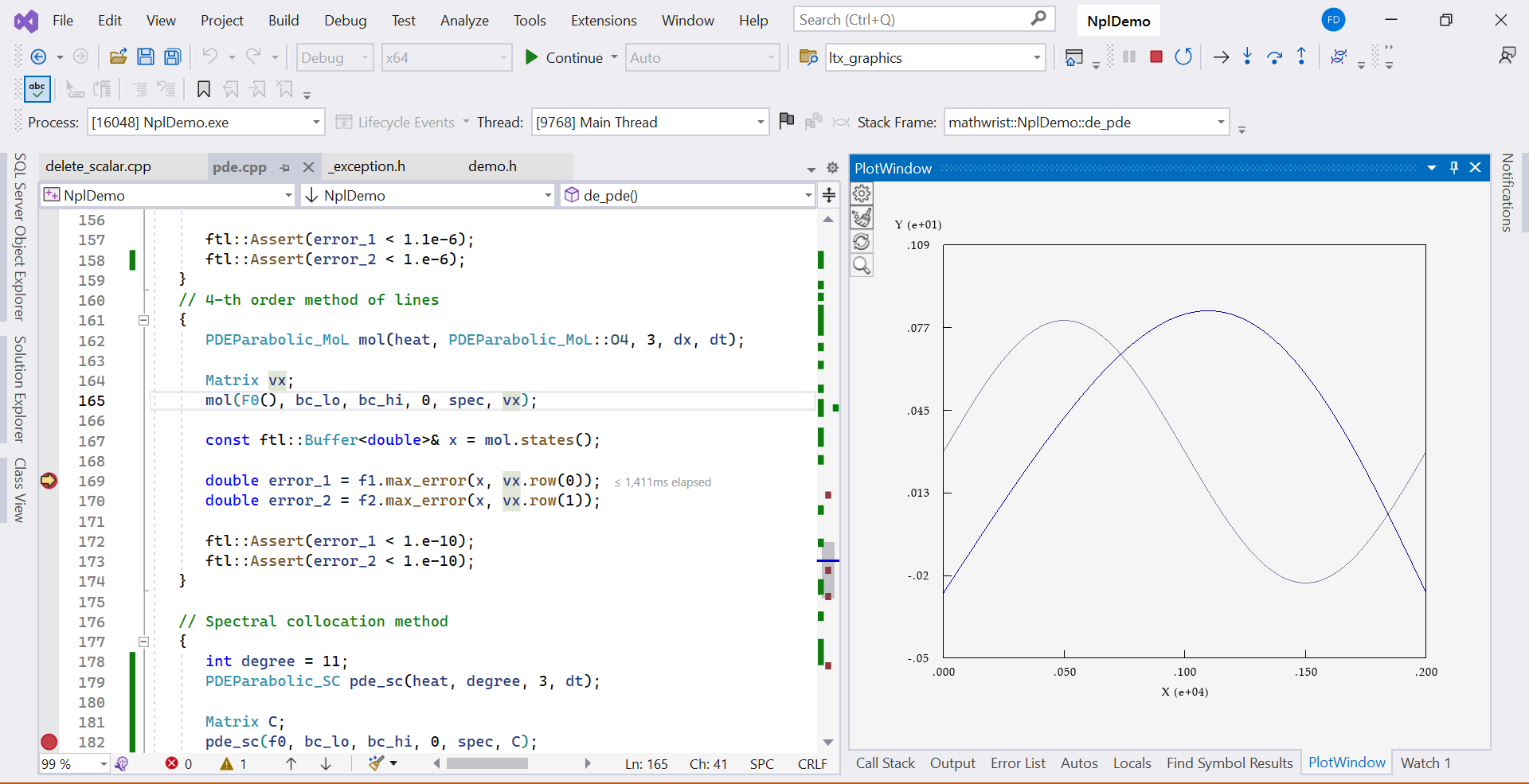
Code blocks from line 135 to 163 use the method of lines with the 2nd order finite difference scheme and the 4th order finite difference scheme. In each case, we use 3 iterations of error correction in implicit IDeC method. The 2nd order method obtains similar result as the Crank-Nicolson method. The 4th order method on the other hand produces 1.e4 times more accurate result. Figure 2 is a plot of the final numerical solutions.

Finally code block between line 165 and 206 illustrates the spectral collocation method, where we choose Chebyshev approximation polynomial of degree 11 and 3 error correction iterations. Note that the output matrix C at line 170 consists of two rows of Chebyshev basis coefficients. We need construct 2 Chebyshev approximation polynomials with these coefficients at line 175 and 180 in order to compute the actual numerical solutions. Code block 182 to 197 uses these two approximation polynomials to evaluate the maximum numerical error over 100 discrete points. As we can see from Figure 1, the initial values are very oscillating. Chebyshev collocation method is not a good choice for this situation. Not surprisingly, Chebyshev collocation method produces large error for not very smooth functions.